Unsicherheiten bei der Vorhersage - Modellunsicherheiten

Der tägliche Wetterbericht gibt Auskunft über die nächsten Tage. Wahrscheinlich interessiert sich ein Großteil der Menschen dafür, ob sie einen Regenschirm brauchen oder nicht. Natürlich gibt es Menschen, die sind auf weitaus mehr angewiesen. Steht ein Sturm vor der Türe, muss man natürlich wissen, wo dieser seinen Schwerpunkt haben wird. Daher ist eine gute Prognose wichtig.

Für die Wettervorhersage sind Modelle ein wesentlicher Baustein. Sie bilden das Fundament, auf dem Meteorologen und Meteorologinnen ihre Vorhersage erstellen. Nicht immer ist nur das Modell oder die große Bandbreite der Modelle entscheidend. In kniffligen Situation ist es auch die Erfahrung des Meteorologen oder der Meteorologin, die den Unterschied macht. Einschätzungen über die Güte der Modelle ist von enormem Vorteil. Dabei hilft es, etwas über Unsicherheiten zu wissen.

Was ist überhaupt ein Modell?

Modelle finden wir eigentlich überall, ob nun in der Meteorologie oder im Finanzwesen. Im Grunde sind Modelle ein Abbild eines Systems. Dabei können sie physisch oder abstrakt sein. Physische Modelle sind haptisch und in den allermeisten Fällen in (viel) kleinerem Maßstab als das Original. Denken Sie nur an den Modellbau. Sei es jetzt Flugzeuge oder Eisenbahnen im kleinen Maßstab. Sie sind Abbilder der Realität, mal mit mehr oder mal weniger Detailtreue, mal mit mehr oder weniger Funktionen. Abstrakte Modelle hingegen sind zum Beispiel mathematischer Natur. Mithilfe von Gleichungen sollen Prozesse beschrieben werden. Dies können Beispiele aus der Ökonomie sein oder eben auch aus der Meteorologie und Klimatologie. Ähnlich wie physische Modelle können sie sich durch den Detailgrad unterscheiden.

So berechnen Wettermodelle Budgets von Masse, Impuls und Energie auf Grundlagen der Erhaltungssätze, wie sie die Physik kennt. So wissen wir, dass Energie erhalten bleibt, also weder erzeugt noch zerstört wird. Wir können mit Gleichungen beschreiben, wie Fluide, so wie es Wasser oder Luft sind, sich verhalten. Wettermodelle simulieren z.B. wie sich Fluide bewegen, interagieren und Wärme austauschen. Kurz zusammengefasst: wie sich die Atmosphäre verhält.

Die Atmosphäre kann nun in ihrer Gesamtheit nicht einfach so simuliert werden. Die Atmosphäre muss dafür unterteilt, also nur an Stichpunkten der Atmosphäre simuliert werden. Die Welt wird durch ein virtuelles „Netz“ überspannt. Das Netz (ob rechteckig oder dreieckig) überspannt die Welt im Modell nicht nur horizontal, sondern auch vertikal. Dabei ist die Auflösung, also die Dichte des Netzes, ausschlaggebend. Je feiner das Netz, desto besser kann die Atmosphäre mit all ihren Phänomenen (z.B. Gewitter) simuliert werden. Aber das ist nicht alles.

Unsicherheit ist ein steter Begleiter von Modellen

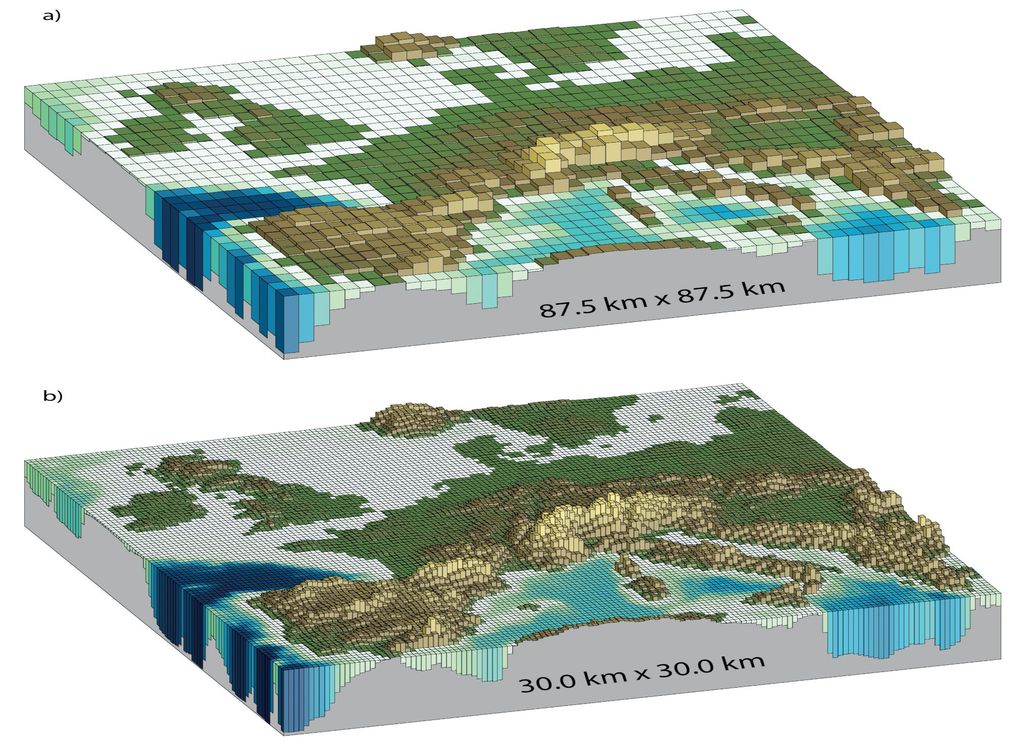
Es fängt damit an, ob der zu beschreibende Prozess überhaupt ausreichend beschrieben werden kann. Jetzt ist es so, dass die oben beschriebenen Prozesse, also das Verhalten von Fluiden, sehr gut mit Gleichungen beschrieben und abgebildet werden können. Bei Modellen der Wettervorhersage spielt allerdings die Auflösung, also wie feinmaschig das oben beschrieben Netz ist, eine wesentliche Rolle. Es gibt Prozesse, die sind in Wirklichkeit kleiner, als das Netz mancher Modelle – beispielsweise Gewitter. Diese Prozesse laufen „subskalig“ ab, also in Größenordnungen, die vom Modell allein durch die Auflösung nicht dargestellt werden können. In diesem Fall muss der Prozess parametrisiert werden, also anders beschrieben werden, damit er vom Modell simulert werden kann. Hierfür verwendet jedes Modell zum Teil andere Parametrisierungen, die den subskaligen Prozess mal besser oder mal weniger besser abbilden kann. Es entsteht also eine Unsicherheit durch diese Prozesse.

So werden in Modellen mit sehr grober Auflösung Gewitter nicht explizit simuliert. Im Modell gewittert es also nicht so wie wir es von der Wirklichkeit kennen. Wir wissen, dass Gewitter dazu da sind, Energieunterschiede auszugleichen. Kann das in einem Modell nicht simuliert werden, kann den zu unsinnigen Ergebnissen führen. Daher ist es nötig, diesen Prozess anders darzustellen, also parametrisiert zu werden. In unserem Beispiel des Gewitters, werden diese in Modellen mit sehr grober Auflösung durch eine teils vereinfachte Beschreibung dargestellt.

Im vorliegenden Beispiel bezüglich der Gewitter weiß man zum Beispiel, dass es Modelle gibt, die unter- oder überschätzen die Gewitteraktivität. Hierfür benötigt es oft die Erfahrung, die eine Einschätzung über eine Gewitterlage sicher ermöglicht. Manchmal ist es dafür nötig, sich andere Parameter anzuschauen, als zum Beispiel die "Gewitteraktivität" im Modell. Daraus kann man wieder Schlüsse für die Zukunft ziehen.

Eine super feine Auflösung birgt den riesigen Vorteil, dass diese Prozesse wieder explizit, also skalig vom Modell beschrieben werden können. Parametrisierungen fallen weg und ebenso die Unsicherheit aus diesen. Der Nachteil daraus ergibt sich aus der Rechenleistung, die dafür nötig ist. Eine höhere Auflösung bedeutet eben auch, dass man an mehr Punkten die Gleichungen lösen muss. Dennoch wird man, auch dank der enormen Rechenleistungen, die mittlerweile möglich sind, auch auf globaler Skala immer weiter die Auflösung erhöhen können.

Das gilt auch für Klimamodelle. Die grundlegenden Prinzipien sind dieselben wie beim Wettermodell. Kann man sich auch leicht vorstellen, warum sollten beim Klima auf einmal andere Grundgleichungen gelten? Eben. Die Wetterprognose hat eine grundlegende Unsicherheit – die Anfangswerte. Die Klimaprognose, eine weitere – das Szenario. Wie das unter einen Hut geht, wird im zweiten Teil erklärt.